El teorema de Thévenin según la teoría de circuitos eléctricos, establece que si una parte de un circuito eléctrico lineal está comprendida entre dos terminales A y B, esta parte en cuestión puede sustituirse por un circuito equivalente que esté constituido únicamente por un generador de tensión en serie con una resistencia, de forma que al conectar un elemento entre los dos terminales A y B, la tensión que queda en él y la intensidad que circula son las mismas tanto en el circuito real como en el equivalente.
El teorema de Thévenin fue enunciado por primera vez por el científico alemán Hermann von Helmholtz en el año 1853, pero fue redescubierto en 1883 por el ingeniero de telégrafos francés Léon Charles Thévenin (1857–1926), de quien toma su nombre. El teorema de Thévenin es el dual del teorema de Norton.
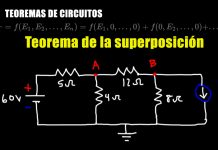
Teorema de Thévenin
El teorema de Thévenin establece que cualquier circuito lineal activo (*) con terminales A y B como el representado en la figura (1), equivale, o puede sustituirse por una fuente de tensión U’ en serie con una impedancia Z’ (figura (2)).
La tensión equivalente de Thevenin U’, es la tensión entre los terminales de A y B medida a circuito abierto (sin carga entre A y B) y la impedancia equivalente Z’ es la impedancia entre los terminales A y B con todas las fuentes internas iguales a cero (cortocircuitadas).
La polaridad de U’ se elige de tal forma que la corriente en una impedancia que se conecte entre A y B tenga el mismo sentido que si dicha impedancia se conectara al circuito activo.
De esta forma, cualquiera sea el circuito lineal activo antes de los terminales A y B, se puede calcular en forma sencilla la corriente que circula por una impedancia conectada a estos terminales mediante la resolución de un circuito serie tal como el de la figura (3).
(*) Circuito lineal activo: es aquel en el cual la tensión y la corriente son directamente proporcionales (lineal) y en el que están presentes fuentes de tensión o de corriente (activo).
Cálculo de la tensión y resistencia de Thévenin
Para calcular la tensión de Thévenin, Vth, se desconecta la carga (es decir, la resistencia de la carga) y se calcula VAB. Al desconectar la carga, la intensidad que atraviesa Rth en el circuito equivalente es nula y por tanto la tensión de Rth también es nula, por lo que ahora VAB = Vth por la segunda ley de Kirchhoff.
Debido a que la tensión de Thévenin se define como la tensión que aparece entre los terminales de la carga cuando se desconecta la resistencia de la carga también se puede denominar tensión en circuito abierto.
Para calcular la resistencia de Thévenin, se desconecta la resistencia de carga, se cortocircuitan las fuentes de tensión y se abren las fuentes de corriente. Se calcula la resistencia que se ve desde los terminales AB y esa resistencia RAB es la resistencia de Thevenin buscada Rth = RAB
En primer lugar, se calcula la tensión de Thévenin entre los terminales A y B de la carga; para ello, se desconecta RL del circuito (queda un circuito abierto entre A y B). Una vez hecho esto, podemos observar que la resistencia de 10 Ω está en circuito abierto y no circula corriente a través de ella, con lo que no produce ninguna caída de tensión. En estos momentos, el circuito que se necesita estudiar para calcular la tensión de Thévenin está formado únicamente por la fuente de tensión de 100 V en serie con dos resistencias, una de 20 Ω y otra de 5 Ω. Como la carga RL está en paralelo con la resistencia de 5 Ω (recordar que no circula intensidad a través de la resistencia de 10 Ω), la diferencia de potencial entre los terminales A y B es igual que la tensión que cae en la resistencia de 5 Ω (ver también Divisor de tensión), con lo que la tensión de Thévenin resulta:
Para calcular la resistencia de Thévenin, se desconecta la carga RL del circuito y se anula la fuente de tensión sustituyéndola por un cortocircuito. Si se colocara una fuente de tensión (de cualquier valor) entre los terminales A y B, veríamos que las tres resistencias soportarían una intensidad. Por lo tanto, se halla la equivalente a las tres: las resistencias de 20 Ω y 5 Ω están conectadas en paralelo y estas están conectadas en serie con la resistencia de 10 Ω, entonces:
